Quỹ tích là phần kiến thức quan trọng trong chương trình Toán Học lớp 9. Vậy quỹ tích là gì? Phương pháp giải bài tập về quỹ tích như thế nào? Hãy cùng supperclean.vn tìm hiểu chi tiết về chủ đề này trong bài viết dưới đây nhé!
Contents
Quỹ tích là gì?
Quỹ tích là tập hợp các điểm cùng thỏa mãn một hoặc nhiều tính chất nhất định nào đó. Tập hợp tìm được có thể là vô hạn (đoạn thẳng, đường thẳng, đường tròn) hoặc hữu hạn (một vài điểm rời rạc) hoặc cũng có thể là tập hợp rỗng (không chứa bất kỳ phần tử nào).
Trong tiếng Anh, quỹ tích được viết là locus.
Các ví dụ minh họa về quỹ tích
Ví dụ 1: Tập hợp các điểm cách đều hai mút của đoạn thẳng là đường trung trực của đoạn thẳng đó.
- Tính chất của quỹ tích: Những điểm cách đều hai đầu đoạn thẳng.
- Tập hợp tìm được: Những điểm thuộc đường trung trực của đoạn thẳng. Đây là một tập vô hạn, tức là có rất nhiều phần tử.
Ví dụ 2: Quỹ tích các điểm M cách O một khoảng cố định OM = R là đường tròn (O;R).
- Tích chất quỹ tích: Tất cả những điểm M cách O một khoảng OM = R (R luôn cố định)
- Tập hợp tìm được: Đường tròn tâm O, bán kính R. Đây cũng là một tập vô hạn các phần tử.
Ví dụ 3: Tập hợp các điểm M cách đường thẳng d cho trước một khoảng không đổi bằng a là đường thẳng d’ song song với d và cách d một khoảng bằng a.
- Tính chất quỹ tích: Những điểm M cách đường thẳng d một khoảng a không đổi
- Tập hợp tìm được: Đường thẳng d’ song song với đường thẳng d và cách d khoảng a không đổi.
Các bước giải bài toán quỹ tích là gì?
Quỹ tích là một dạng bài tập khó, phức tạp, đòi hỏi người đọc dành nhiều thời gian và vận dụng nhiều kiến thức khác nhau. Dưới đây là các bước khi làm bài toán quỹ tích:
Bước 1: Dự đoán quỹ tích
Bước này vô cùng quan trọng vì nó sẽ quyết định đến định hướng giải bài toán. Bạn có thể dự đoán quỹ tích qua các phương pháp sau:
(*) Phương pháp thực nghiệm:
Đây là phương pháp thông dụng và được áp dụng nhiều nhất. Ta có thể dựa vào đặc điểm các đặc điểm sau để dự đoán:
- Nếu quỹ tích có 3 điểm thẳng hàng thì quỹ tích có thể thuộc tia, đường thẳng hoặc đoạn thẳng.
- Nếu quỹ tích không có 3 điểm thẳng hàng thì quỹ tích có thể thuộc nửa đường tròn, cung tròn hoặc đường tròn.
Để dự đoán quỹ tích chính xác nhất, bạn cần lưu ý các yếu tố sau:
- Yếu tố cố định, không thay đổi
- Yếu tố tạo ra quỹ tích
- Yếu tố quỹ tích
Trong một bài toán sẽ có nhiều yếu tố khác nhau. Vì vậy, ta chỉ cần tập trung vào những yếu tố liên quan để giải bài tập. Hơn nữa, đôi khi các yếu tố đặc trưng không được thể hiện trực tiếp nên nếu muốn hiểu được thì cần phải có tư duy linh hoạt và sáng tạo.
Ví dụ 4: Một điểm A nằm ngoài đường thẳng d (cố định) và điểm B di động thuộc d. Hãy tìm quỹ tích trung điểm M của đoạn thẳng AB.
Lời giải:
Theo bài toán trên, ta có:
- Yếu tố cố định: đường thẳng d, điểm A nằm ngoài d
- Yếu tố sinh ra quỹ tích: điểm B
- Yếu tố quỹ tích: điểm M (trung điểm của AB)
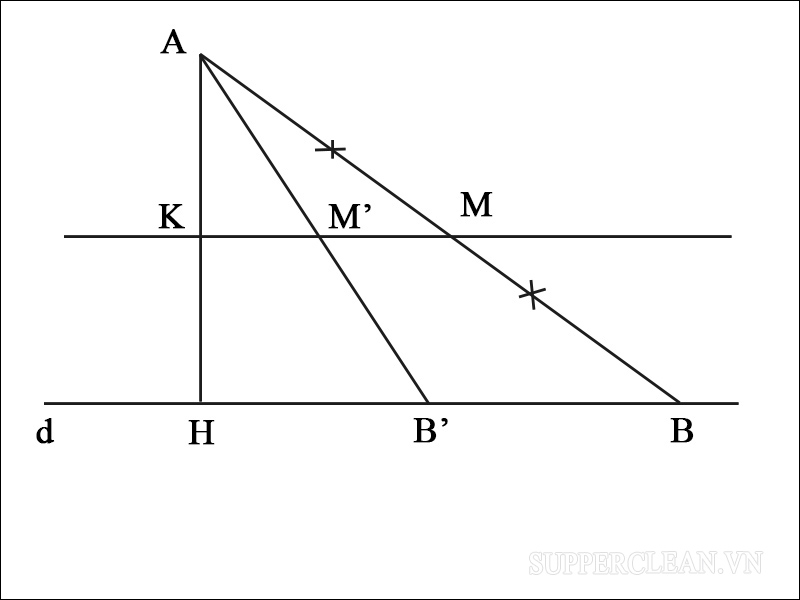
Với vị trí điểm B như hình vẽ, M là trung điểm của AB. Hình chiếu của điểm A trên đường thẳng d là điểm H.
Khi B trùng với H thì M trùng K (K: trung điểm của AH).
Khi B trùng với B’ thì M sẽ trùng với M’.
Từ đó, ta thấy M, M’, K thẳng hàng nên quỹ tích M sẽ là đường thẳng.
(*) Dựa vào số lượng giao điểm của quỹ tích với đường thẳng cố định
Kẻ đường thẳng d cố định. Nếu quỹ tích chỉ có 1 điểm chung với d thì quỹ tích thuộc đường thẳng. Ngược lại, nếu quỹ tích có hai điểm chung với d thì quỹ tích thuộc đường tròn.
Ví dụ 5: Cho A và B là hai điểm cố định. Hãy xác định quỹ tích điểm M sao cho MA = MB.
Dự đoán: Trên đường thẳng AB có 1 điểm M1 thỏa mãn điều kiện M1A = M1B. Vì vậy, M1 là trung điểm của AB.
=> Qũy tích điểm M chỉ có 1 giao điểm với AB => Qũy tích thuộc loại thẳng.
(*) Dựa vào tính chất đối xứng
Nếu một đường thẳng x vuông góc với d thì x sẽ nhận d là trục đối xứng và ngược lại. Nếu đường tròn (O) nhận d làm trục đối xứng thì tâm O sẽ nằm trên đường thẳng d.
Từ đó, ta có kết luận sau:
- Nếu quỹ tích thuộc loại thẳng và nhận đường thẳng d là trục đối xứng thì quỹ tích thuộc đường thẳng vuông góc với d.
- Nếu quỹ tích thuộc loại tròn và nhận đường thẳng d làm trục đối xứng thì tâm của đường tròn nằm trên d.
Xét ví dụ 8, ta thấy: Về cả hai phía của đường thẳng AB bao giờ cũng có hai điểm M và M’ thỏa mãn MA = MB = M’A = M’B.
=> Quỹ tích điểm M có tính chất MA = MB là một đường thẳng vuông góc với AB.
=> Quỹ tích điểm M là một đường thẳng vuông góc với AB.
(*) Dựa vào phần tử xa vô tận
Theo hình học phi Ơ – clit, ta có:
- Mỗi đường thẳng được xem là có một điểm ở xa vô tận
- Hai đường thẳng song song sẽ cắt nhau tại một điểm xa vô tận.
Từ đó, ta rút ra kết luận sau:
- Quỹ tích có 1 điểm ở xa vô tận thì quỹ tích thuộc loại thẳng.
- Nếu quỹ tích không có điểm ở xa vô tận thì quỹ tích thuộc loại tròn hoặc là một phần của đường thẳng.
Ví dụ 9: Đường tròn (O) và điểm cố định I nằm trong đường tròn. Đường thẳng d đi qua điểm I và cắt (O) tại A và B. Tiếp tuyến tại A và B giao nhau tại điểm M. Hãy xác định quỹ tích điểm M.
Lời giải:
Khi d trùng với IO thì d sẽ giao với đường tròn (O) tại hai điểm A1 và B1. Khi đó, hai tiếp tuyến tại A1 và B1 sẽ song song với nhau và cắt nhau tại điểm M vô tận.
=> Quỹ tích điểm M là đường thẳng và nhận OI làm trục đối xứng (do về hai phía của IO luôn có hai điểm M1 và M2 thuộc quỹ tích đối xứng nhau qua OI)
=> Quỹ tích M là đường thẳng vuông góc với IO.
Chứng minh phần thuận
Bước dự đoán quỹ tích được làm ra nháp. Bắt đầu từ phần “chứng minh phần thuận” sẽ được trình bày vào bài làm.
Quy tắc chứng minh: Mọi điểm M có tính chất T đều sẽ thuộc hình H. Hay nói cách:
M ⊂ T => M ⊂ H
Do điểm M thuộc T nên M có tính chất . Ta sẽ chia nhỏ tính chất thành các tính chất nhỏ hơn như 1, 2, 3,… Sau đó, dựa vào các tính chất và định lý hình học để xác định xem M có các tính chất 1, 2, 3,… hay không? Nếu có thì M ⊂ H.
Xác định giới hạn
Căn cứ vào vị trí của M, hãy chứng tỏ M chỉ thuộc H hoặc một phần của hình H.
Chứng minh phần đảo
Lấy điểm M thuộc hình H (đã giới hạn quỹ tích). Giả sử, tính chất T có n điều kiện. Khi đó, hãy dựng một hình để chứng minh M có tính chất T sao cho M thỏa mãn n điều kiện là được.
Kết luận
Bước cuối cùng khi giải bài toán quỹ tích là kết luận. Kết luận quỹ tích điểm M là hình H. Đồng thời nêu rõ hình dạng cũng như cách xác định hình H.
Bài tập minh họa về quỹ tích
Để bạn đọc hiểu rõ hơn về khái niệm quỹ tích là gì và cách giải, chúng ta sẽ cùng nhau giải bài tập dưới đây:
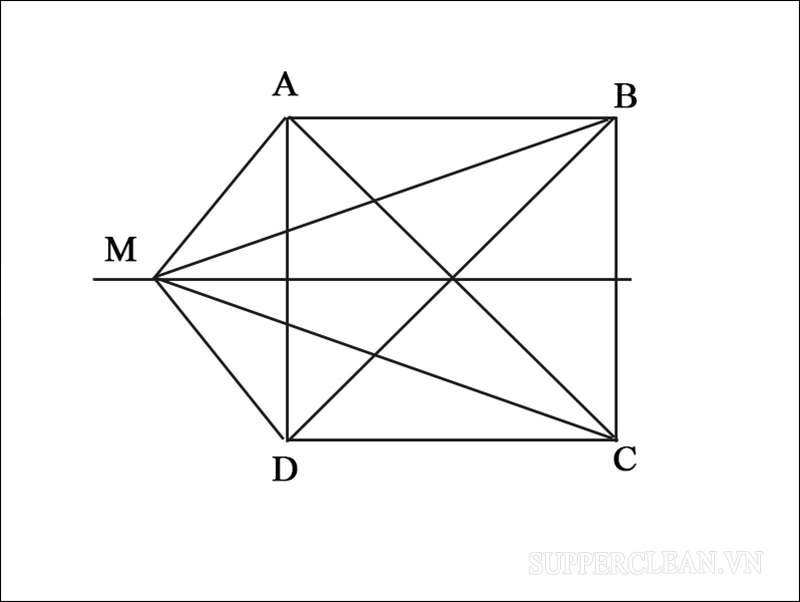
Bài tập số 1: Cho hình vuông ABCD, hãy tìm tập hợp điểm M trong mặt phẳng sao cho MA + MB = MC + MD.
Lời giải:
(*) Chứng minh phần thuận:
Ta kẻ đường thẳng d đi qua tâm O của hình vuông và song song với DC, AB. Khi đó, d là đường trung trực của BC và AB.
Với mọi điểm M không thuộc d thì MA + MB # MC + MD. Đồng thời:
MA + MB > MC + MD khi M nằm khác phía với điểm A so với d.
MA + MB < MC + MD khi M nằm cùng phía với A so với đường thẳng d.
=> Để MA + MB = MC + MD thì M phải thuộc đường trung trực d của BC và AD.
(*) Giới hạn
Mọi điểm M thuộc đường thẳng d đều có MA = MD và MC = MB
=> MA + MB = MC + MD => M thuộc d.
(*) Chứng minh phần đảo
Lấy điểm M bất kì thuộc d, ta có: MA = MD, MB = MC.
Khi đó, MA + MB = MC + MD.
Vậy tập hợp điểm M cần tìm sẽ là đường trung trực của AD và BC.
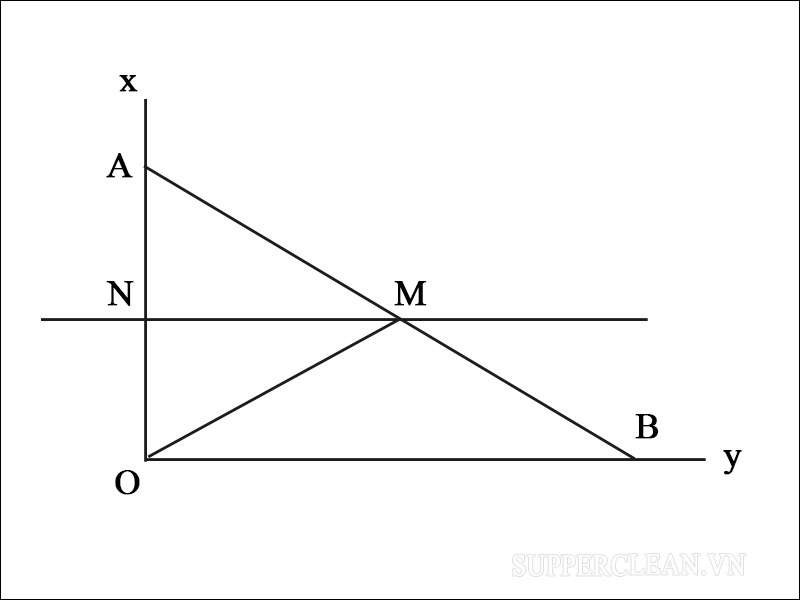
Bài tập số 2: Cho góc xuống xOY cố định, điểm A cố định trên Oy và điểm B di động trên Ox. Hãy xác định tập hợp trung điểm M của đoạn thường AB?
Lời giải:
(*) Chứng minh phần thuận
Ta có: OM = AB/2, MA = AB/2
=> MA = OM (không đổi)
Điểm M cách đều O và A (O, A cố định) nên M thuộc đường trung trực của OA.
(*) Giới hạn
Vì AB thuộc miền trong của xOy nên M nằm trên tia Nm. Nm thuộc đường trung trực của OA và nằm trong góc xOy (N: trung điểm của OA).
(*) Chứng minh phần đảo
Lấy M thuộc tia Mn, AM cắt Ox tại điểm B. Khi đó ta có:
M’A = M’O => Tam giác MOA cân tại đỉnh M
=> ∠ MAO = ∠ MOA
Mà ∠MOA + MOB = 90 và MAO + MBO = 90.
=> MOB = MBO => Tam giác MOB cân tại đỉnh M.
=> MO = MB => MA = MB.
=> M là trung điểm của AB.
Vậy khi M di chuyển di động trên tia Ox thì các trung điểm M của AB là tia Nm thuộc đường trung trực OA và thuộc miền trong của góc xOy, với N là trung điểm của đoạn OA.
XEM THÊM:
Trên đây là bài viết chia sẻ kiến thức về quỹ tích là gì, cách giải và bài tập minh họa. Hy vọng sẽ giúp ích thật nhiều cho bạn đọc trong quá trình học tập và ôn luyện nhé!