Giai thừa là phép tính xuất hiện nhiều trong bài thi môn Toán của kỳ thi THPT Quốc Gia. Vậy giai thừa là gì? Cách tính giai thừa như thế nào? Mời bạn đọc cùng supperclean.vn ôn luyện kiến thức về giai thừa trong bài viết dưới đây nhé!
Contents
Giai thừa là gì?
Giai thừa là phép toán học tính tích của dãy số tự nhiên liên tiếp từ 1 đến số cần tính giai thừa. Ký hiệu giai thừa là dấu chấm than (!). Với n là số tự nhiên dương. Khi đó, n giai thừa là tích của dãy số tự nhiên liên tiếp từ 1 đến n. Ký hiệu là n!.
Ví dụ về giai thừa:
- 5 giai thừa viết là 5!
- 7 giai thừa viết là 7!
- 1 giai thừa viết là 1!
- 10 giai thừa viết là 10!
- (n + 1) giai thừa viết là (n+1)!

Cách tính giai thừa là gì?
Cho n là số tự nhiên dương. Vậy n giai thừa bằng gì? Dưới đây là công thức tổng quát chung:
n! = n x (n – 1) x (n – 2) x …. x 2 x 1 (Điều kiện: n ≥ 0, n ∈ N)
Hoặc:
n! = 1 x 2 x …. x (n – 2) x (n – 1) x n (Điều kiện: n ≥ 0, n ∈ N)
Để hiểu rõ hơn về cách tính giai thừa, bạn đọc hãy tham khảo các ví dụ dưới đây:
- 2! = 2 x 1 = 2
- 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720
- 3! = 3 x 2 x 1 = 6
- 4! = 4 x 3 x 2 x 1 = 24
- 3! + 4! = 3 x 2 x 1 + 4 x 3 x 2 x 1 = 6 + 24 = 30
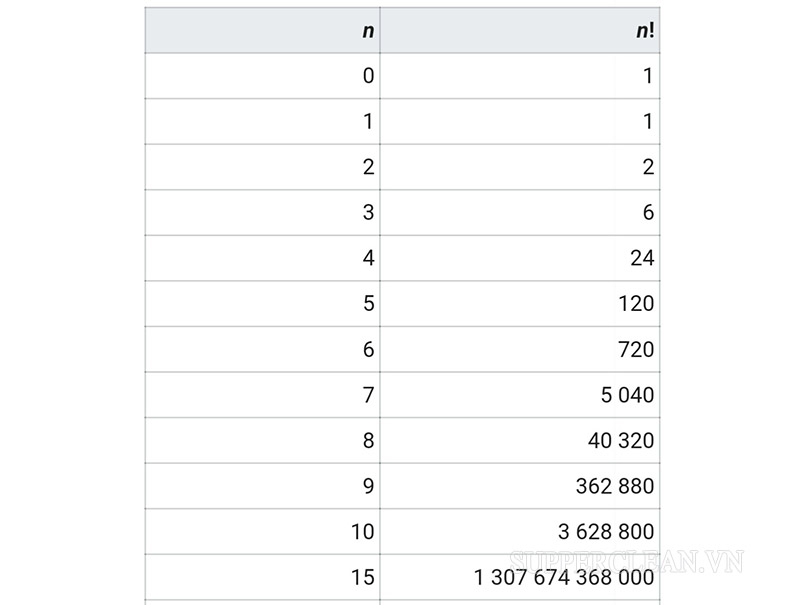
Tính chất của giai thừa là gì?
Để giải quyết các bài tập về giai thừa, chúng ta cần nắm vững các tính chất sau:
- Quy ước: 0! = 1
- n! = (n – 1)! x n (1 ≤ n ∈ N) (Phát biểu bằng lời: Giai thừa lớn có thể biểu diễn thông qua các giai thừa nhỏ hơn). Ví dụ: 5! = (4!) x 5, 10! = (9!) x 10, 45! = (44!) x 45,…
Các câu hỏi thắc mắc về giai thừa
5 giai thừa bằng bao nhiêu?
5 giai thừa là gì? 5 giai thừa là tích các số tự nhiên liên tiếp từ 1 đến 5. 5 giai thừa được tính như sau:
5! = 5 x 4 x 3 x 2 x 1 = 120
Vậy 5 giai thừa bằng 120.
1 giai thừa bằng bao nhiêu?
Áp dụng cách tính giai thừa, ta có:
1! = 1
Trong khi đó, 0! = 1 (quy ước). Điều này khiến cho nhiều người thắc mắc vì sao 0! được quy ước là 1 mà 1! cũng bằng 1. Cách lý giải cụ thể như sau:

(n+1) giai thừa bằng gì?
Theo quy tắc giai thừa lớn có thể biểu diễn thông qua giai thừa nhỏ hơn, ta có:
(n + 1)! = (n!) x (n + 1) vì n < n + 1 với (0 ≤ n ∈ N)
(n – 1) giai thừa bằng gì?
Ta có:
(n – 1)! = (n – 1) x (n – 2) x (n – 3) x …. 3 x 2 x 1 = n!/n
(n-2) giai thừa bằng gì?
Tương tự như cách triển khai trên, ta có:
(n – 2)! = n!/ [n x (n – 1)]
7 giai thừa bằng bao nhiêu?
7! = 1 x 2 x 3 x 4 x 5 x 6 x 7 = 5.040
Vậy 7 giai thừa bằng 5.040.
Giao thừa kép là gì?
Với n là số tự nhiên, giai thừa kép của n (ký hiệu n!!) được định nghĩa như sau:
- Với n = 1 hoặc n = 0 thì n!! = 1
- Với n ≥ 2 thì n!! = 1 x 3 x 5 x 7 x … x n (khi n là một số lẻ) hoặc n!! = 2 x 4 x 6 x … x n (khi n là một số chẵn)
Ví dụ:
4!! = 2 x 4 = 8
6!! = 2 x 4 x 6 = 48
12!! = 2 x 4 x 6 x 8 x 10 x 12 = 46.080
Siêu giai thừa là gì?
Siêu giai thừa được định nghĩa là tích của n giai thừa đầu tiên. Với n là số tự nhiên, siêu giai thừa của n được ký hiệu là sf(n) và tính theo công thức sau:
sf(n) = 1! x 2! x 3! x … x n!
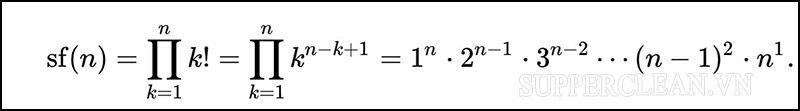
Ví dụ:
sf(4) = 1! x 2! x 3! x 4! = 288
sf(5) = 1! x 2! x 3! x 4! x 5! = 34.560
XEM THÊM:
Các dạng bài tập thường gặp về giai thừa
Dạng 1: Tính giá trị biểu thức
Đây là dạng bài tập cơ bản và đơn giản nhất. Bạn chỉ cần áp dụng cách tính giai thừa và các tính chất liên quan để thực hiện.
Ví dụ: Hãy thực hiện các phép tính sau:
- 5! + 4! – 2! = ?
- (3! x 4!) – (3! – 2!) = ?
- (4! + 5!)/ (1! + 2!) = ?
Lời giải:
Tính nhanh: 1! = 1, 2! = 2, 3! = 6, 4! = 24, 5! = 120
- 5! + 4! – 2! = 120 + 24 – 2 = 142.
- (4! + 2!) – (3! – 1!) = (24 + 2) – (6 – 1) = 26 – 5 = 21
- (4! + 5!)/ (1! + 2!) = (24 + 120) / (1 + 2) = 144/3 = 48
Dạng 2: Rút gọn giai thừa (rút gọn biểu thức)
Dạng này nâng cao hơn một chút với biểu thức có thể là số hoặc ẩn. Với dạng bài tập này, bạn cần áp dụng kiến thức về giai thừa và nhiều kiến thức toán học khác như phân tích biểu thức, giao hoán, kết hợp,… để thực hiện.
Ví dụ minh họa:

Dạng 3: Giải phương trình chứa ẩn trong giai thừa
Đây là dạng bài khó nhất trong giai thừa. Dạng bài tập này yêu cầu người học phải vận dụng thêm nhiều kiến thức và kỹ năng toán học khác.

Như vậy, bài viết trên đã giúp bạn giải đáp số giai thừa là gì và các dạng bài tập thường gặp về giai thừa. Nếu bạn có thắc mắc hay gặp bài tập khó thì hãy bình luận bên dưới để supperclean.vn hỗ trợ giải đáp nhanh nhất nhé!




